Foire Aux Questions
50 questions les plus fréquentes sur les Thermo-couples et les RTD
La température n’est pas une grandeur au sens strict du terme, comme le sont la plupart des autres unités de mesure. En effet, une grandeur est tout ce qui est susceptible d’augmentation ou de diminution comme, par exemple, une longueur, une surface, une puissance, etc.
Mesurer une grandeur G (quelle que soit son espèce), c’est la comparer à une autre grandeur U, de même espèce, choisie pour unité. Le résultat de la mesure est un nombre entier (par exemple 5) si l’unité U est contenue un nombre entier de fois dans la grandeur G considérée (5 fois ici). Une grandeur est directement mesurable quand nous pouvons définir le rapport ou l’égalité ou la somme de deux valeurs de cette grandeur. Une longueur, une surface sont des grandeurs mesurables.
En revanche, une température repérée au moyen de l’échelle thermométrique Celsius n’est pas une grandeur mesurable ; nous pouvons définir l’égalité de deux températures mais nous ne pouvons pas en faire la somme. On devrait donc dire : évaluer, comparer, marquer, indiquer les températures et non pas les mesurer au sens propre du terme.
Il existe actuellement, dans le Système International, deux unités de température :
Le kelvin, symbole K
Degré de l’échelle thermodynamique des températures absolues dans laquelle la température du point triple de l’eau est 273,16 K
Le degré Celsius, symbole °C
La température Celsius t correspondant à la température thermodynamique T est définie par l’équation t = T – T0 dans laquelle T0 = 273,15 K.
Un intervalle ou une différence de température peut aussi s’exprimer en degré Celsius. Dans les siècles passés, plusieurs échelles de mesure des températures furent définies, basées sur deux points fixes ou plus.
Il faut noter que le kelvin doit être utilisé ni avec le mot degré, ni avec le symbole ° ; on dit « un kelvin » et non pas un degré kelvin.
L’ITS (International Temperature Scale) a établi dix-sept points de référence de température, basé sur le phénomène physique du point triple, de la pression de vapeur, du point de congélation, de fusion et de solidification de différents matériaux. Ces points particuliers se produisent à une température fixe et reproductible, déterminée par la Nature. Ils ne nécessitent donc pas l’utilisation d’un capteur étalon pour être mesurés. Par exemple, la fusion (passage de l’état solide à l’état liquide) du Gallium se produit toujours à 29.7646°C. Un point fixe particulier est le point triple. Et un point triple particulier est le point triple de l’eau (0.01°C sous 1 atm).
Le point triple est le point des intersections des courbes d’évaporation, de sublimation et de fusion d’un matériau. C’est Josiah W. Gibbs (1839-1903) qui reconnaît et énonce la règle des phases : les trois états, solide, liquide et gazeux ne coexistent qu’en un point unique de l’espace des paramètres thermodynamiques, le point triple. On pourra trouver ensemble de la vapeur, du liquide et du solide à une température et une pression uniques, parfaitement définies.
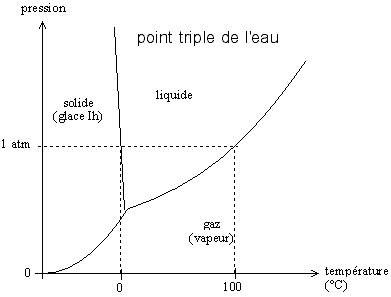
Figure 1. Evolution de la pression avec la température pour le point triple de l’eau
L’ITS (International Temperature Scale) a établi dix-sept points de référence de température :
| Élément | Symbole | Type | K | °C |
| Hélium | He | Pression de vapeur | 5 | -268.15 |
| Hydrogène | H2 | Point triple | 13.8033 | -259.3467 |
| Hydrogène | H2 | Pression de vapeur | 17 | -256.15 |
| Hydrogène | H2 | Pression de vapeur | 20.3 | -252.85 |
| Néon | Ne | Point triple | 24.5561 | -248.5939 |
| Oxygène | O2 | Point triple | 54.3584 | -218.7916 |
| Argon | Ar | Point triple | 83.8058 | -189.3442 |
| Mercure | Hg | Point triple | 234.315 | -38.8344 |
| Eau | H2O | Point triple | 273.16 | 0.01 |
| Gallium | Ga | Fusion | 302.9146 | 29.7646 |
| Indium | In | Congélation | 429.7485 | 156.5985 |
| Étain | Sn | Congélation | 505.078 | 231.928 |
| Zinc | Zn | Congélation | 692.677 | 419.527 |
| Aluminium | Al | Solidification | 933.473 | 660.323 |
| Argent | Ag | Congélation | 1234.93 | 961.78 |
| Or | Au | Congélation | 1337.33 | 1064.18 |
| Cuivre | Cu | Congélation | 1357.77 | 1084.62 |
Dans un circuit fermé constitué de deux conducteurs de nature différente, il circule un courant lorsqu’on maintient entre les deux jonctions une différence de température.

Figure 2 Circuit fermé : schéma du fonctionnement général d’un thermocouple
Circuit coupé : en chauffant la jonction des deux métaux différents A et B, une tension eAB apparaît ; elle est fonction de la température de la jonction et de la composition des deux métaux. Tous les métaux dissemblables présentent cet effet.

Figure 3 Circuit ouvert présentant le fonctionnement général d’un thermocouple
L’apparition de la tension entre des métaux dissemblables dont les extrémités sont à différentes températures est en relation avec les trois effets thermoélectriques dans les métaux :
- L’effet Seebeck : Thomas Johann Seebeck (1770-1831) est le premier à avoir mis en évidence les effets thermoélectriques de production de courants qui se manifestent dans un circuit constitué de deux métaux dont les deux soudures se trouvent à des températures différentes. Il ne manqua pas de noter le phénomène provoqué par une différence de température le long d’un conducteur homogène ; phénomène qui sera redécouvert trente ans plus tard par William Thomson et qu’on appellera Effet Thomson.
- L’effet Peltier : Jean Charles Athanase Peltier, physicien français (1785-1845), abandonne la profession d’horloger à l’âge de trente ans pour se consacrer à la recherche en physique ; il est connu pour sa découverte en 1834 de l’effet Peltier : lorsqu’un courant électrique passe dans une jonction de deux conducteurs de métaux différents, on observe une augmentation ou une baisse de température selon le sens du courant ; la quantité de chaleur dégagée ou absorbée étant proportionnelle à l’intensité du courant. C’est, en quelque sorte, l’inverse de l’effet Seebeck. Le passage d’un courant peut donc absorber de la chaleur ; on utilise cet effet dans certains petits réfrigérateurs ou pour le refroidissement de circuits électriques.
- L’effet Thomson : Découvert par lord Kelvin (alors sir William Thomson) – mais déjà noté par Seebeck -, qui en a reconnu l’existence par expérience après l’avoir démontré théoriquement. C’est une sorte d’effet Peltier, mais entre des portions contiguës d’un même barreau de métal. L’effet Thomson se rapporte à la production – ou à l’absorption – de chaleur provoquée par le passage d’un courant dans une portion de conducteur, en présence d’une différence de température entre les extrémités du tronçon.
La force électromotrice qui apparaît dans le circuit d’un thermocouple dépend de la nature des deux conducteurs et des températures des deux jonctions ; celles-ci sont appelées respectivement :
- Soudure chaude : Jonction de l’ensemble thermocouple soumis à la température à mesurer : c’est la jonction Capteur.
- Soudure froide : Jonction de l’ensemble thermocouple maintenu à une température connue ou à 0 °C : c’est la jonction Référence
On rencontre habituellement 8 types de thermocouples :
| Type | Métal A (+) | Métal B (-) | Limites théoriques | Coef. Seebeck α (µV/°C) à T°C | Erreur standard | Erreur Mini |
| B | Platine 30% Rhodium | Platine 6% Rhodium | 0 à 1820°C | 5,96 µv à 600°C | 0,5% | 0,25% |
| E | Nickel 10% Chrome | Constantan | -270 à 1000°C | 58,67 µV à 0°C | 1,7% à 0,5% | 1% à 0,4% |
| J | Fer | Constantan | -210 à 1200°C | 50,38 µV à 0°C | 2,2% à 0,75% | 1,1% à 0,4% |
| K | Chromel | Alumel | -270 à 1372°C | 39,45 µV à 0°C | 2,2% à 0,75% | 1,1% à 0,2% |
| N | Nicrosil | Nisil | -270 à 1300°C | 25,93 µV à 0°C | 2,2% à 0,75% | 1,1% à 0,4% |
| R | Platine 13% Rhodium | Platine | -50 à 1768°C | 11,36 µV à 600°C | 1,5% à 0,25% | 0,6% à 0,1% |
| S | Platine 10% Rhodium | Platine | -50 à 1768°C | 10,21 µV à 600°C | 1,5% à 0,25% | 0,6% à 0,1% |
| T | Cuivre | Constantan | -270 à 400°C | 38,75 µV à 0°C | 1% à 0,75% | 0,5% à 0,4% |
Les métaux et les alliages utilisés, aux caractéristiques éprouvées, sont normalisés au niveau international, en ce qui concerne les matériaux, les courbes de transfert, les symboles, les tolérances et les codes de couleur suivant des normes :
- CEI 584-1 (ex NF C 42-321) Tables de référence – e = f(Θ)
- CEI 584-2 (ex NF C 42-322) Tolérances
- CEI 584-3 (ex NF C 42-323) Identification des couples thermoélectriques et des câbles de compensation
- CEI 584-4 (ex NF C 42-324) Câbles d’extension et de compensation pour couples thermoélectriques
- CEI 584-5 (ex NF C 42-325) Câbles et thermocouples dits « chemisés »
| Type | Couleurs CEI 584-3 (+ / -) | Couleurs NF C 42-323 1985 (+ / -) | Plages utilisation | Tolérances NF EN 60-584 Classe 1 | Tolérances NF EN 60-584 Classe 2 |
| B | Gris / Blanc | Jaune / Gris | +600 à +1700°C | – | ±0.0025.Θ de 600 à +1700°C |
| E | Violet / Blanc | Jaune / Orange | -40 à +900°C | ±1.5°C de -40 à +375°C ±0.0004.Θ de 375 à 800°C | ±2.5°C de -40 à +333°C ±0.0075.Θ de 333 à 900°C |
| J | Noir / Blanc | Jaune / Noir | -40 à +750°C | ±1.5°C de -40 à +375°C ±0.004.Θ de 375 à 750°C | ±2.5°C de -40 à +333°C ±0.0075.Θ de 333 à 750°C |
| K | Vert / Blanc | Jaune / Violet | -40 à +1200°C | ±1.5°C de -40 à +375°C ±0.004.Θ de 375 à 1000°C | ±2.5°C de -40 à +333°C ±0.0075.Θ de 333 à 1200°C |
| N | Rose / Blanc | – | -40 à +1200°C | ±1.5°C de -40 à +375°C ±0.004.Θ de 375 à 1000°C | ±2.5°C de -40 à +333°C ±0.0075.Θ de 333 à 1000°C |
| R | Orange / Blanc | Jaune / Vert | 0 à +1600°C | ±1.0°C de 0 à +1100°C ±1+0.003.(Θ-1100) de 1100 à 1600°C | ±1.5°C de 0 à +600°C ±0.0025.Θ de 600 à 1600°C |
| S | Orange / Blanc | Jaune / Vert | 0 à +1600°C | ±1.0°C de 0 à +1100°C ±1+0.003.(Θ-1100) de 1100 à 1600°C | ±1.5°C de 0 à +600°C ±0.0025.Θ de 600 à 1600°C |
| T | Brun / Blanc | Jaune / Bleu | -40 à +350°C | ±0.5°C de -40 à +125°C ±0.004.Θ de 125 à 350°C | ±1.0°C de -40 à +133°C ±0.0075.Θ de 133 à 350°C |
Le constantan est un alliage de cuivre et de nickel caractérisé par une résistance électrique pratiquement indépendante de la température, et convenant donc à la construction de résistances électriques. Le cuivre et le nickel étant deux métaux parfaitement isomorphes, ils sont donc miscibles à l’état liquide en toutes proportions. La courbe des conductivités de l’alliage, en fonction de la proportion de cuivre et de nickel, présente un aspect typique avec un minimum très accentué autour du point 50%, et une croissance très rapide lorsqu’on approche des métaux purs. Dans la pratique, on utilise généralement un alliage à 60% de cuivre et 40% de nickel, d’une résistance spécifique de 0,5 Ω/mm²/m.
Ces deux métaux peuvent également former un alliage par simple diffusion sans passer par la phase liquide. L’expérience a été réalisée par Bruni, qui chauffait un fil de cuivre sur lequel avait été déposée une couche de nickel. La résistance de l’ensemble augmentait très nettement par suite de la formation du constantan. ATTENTION : Constantan est le nom générique des alliages de cuivre et de nickel et ne donne pas un pourcentage précis des deux métaux. Le Constantan utilisé dans les thermocouples de type T (Cuivre/Constantan) n’est pas le même que celui des thermocouples de type J (Fer/Constantan).
Bien qu’ils soient donnés pour une plage théorique de 0 à 1820°C, les thermocouples de type B présentent une zone de difficulté de calcul et d’incertitude entre 0 °C et 100 °C pour laquelle la tension thermoélectrique fluctue entre -0.003 mV et +0.003 mV (0 à 50 °C) puis croît très doucement jusqu’à 0.033 mV à 100 °C. Pour pouvoir effectuer des calculs avec certitude et obtenir une précision de 1 °C dans cette zone, il serait nécessaire de disposer d’un moyen de mesure d’une résolution d’au moins 0.01 µV pour une précision de 0.1 µV, mais la table ITS-90 pour le type B ne donne qu’une précision de 1 µV. La plage d’utilisation normalisée est de +600 à +1700°C. Les limites basses seront donc de 100 °C ou 0.033 mV pour les calculs.
Les thermocouples de type B sont communément nommés : Thermocouples 18% (Explication : 30% Rhodium (Positif) + 6% Rhodium (Négatif) égale 36% qui divisé par deux donne 18%).
Il existe d’autres types de thermocouples, comme ceux à base de Tungstène (W) allié avec du Rhénium (Re) pour le rendre un peu plus malléable. Ils sont utilisés pour les très hautes températures dans le vide ou en atmosphère inerte. Ce sont les type C (W-5%Re/W-26%Re), type D (W-3%Re/W-25%Re) et type G (W/W-26%Re).
Pour de petits changements de température, la variation de tension est proportionnelle à la variation de température. Le coefficient de proportionnalité est appelé coefficient de Seebeck et noté α.
Un des thermocouples le plus utilisé est le Chromel-Alumel ou Thermocouple de Type K. Il possède une plage de mesure étendue (-100 à + 1370 °C), une force électromotrice importante (41310 µV à 1000 °C avec soudure froide à 0°C) et une courbe que l’on sait très bien linéariser pour obtenir sur toute l’étendue de mesure des précisions meilleures que 0,2%. Le thermocouple type K est composé d’alumel : alliage composé de 95% de nickel, 2% d’aluminium, 2% de manganèse et 1% de silicium et de Chromel : Alliage composé de 80% de nickel et 20% de Chrome.
Maintenant que nous savons qu’un thermocouple génère une tension dont la valeur est fonction de la température et du coefficient de Seebeck (α) de la jonction des deux métaux dissemblables, il ne reste plus qu’à mesurer celle-ci à l’aide d’un voltmètre puis d’exprimer, par calcul, la tension mesurée en température.
Connexion sur un voltmètre
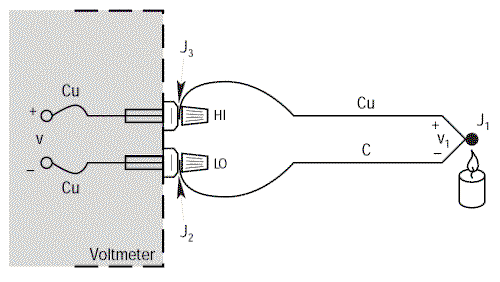
Connectons un thermocouple Cuivre/Constantan (Type T) sur les bornes d’un voltmètre et, après calcul d’après α = 38,75µV/°C, nous trouvons une valeur de température qui n’a rien à voir avec l’ambiance dans laquelle se trouve le thermocouple.
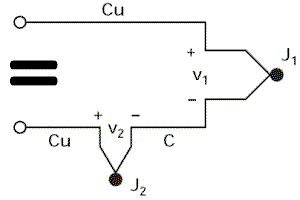
En fin de compte, en se référant au schéma équivalent (=), la tension résultante mesurée par le voltmètre est égale à V1 – V2, c’est-à-dire qu’elle est proportionnelle à la différence de température entre J1 et J2.
Nous ne pourrons trouver la température de J1 que si nous connaissons celle de J2
Référence de la jonction externe
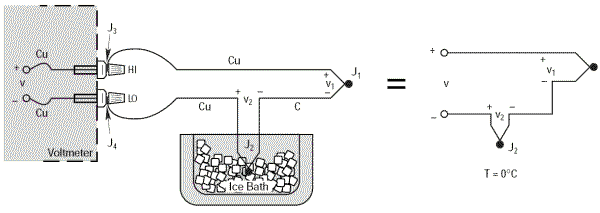
Une manière simple de déterminer exactement et facilement la température de la jonction J2 est de la plonger dans un bain de glace fondante, ce qui force sa température à 0°C (273,15 K). On pourra alors considérer J2 comme étant la jonction de référence. Le schéma a donc maintenant une référence 0°C sur J2.
Et avec un autre type de thermocouple ?
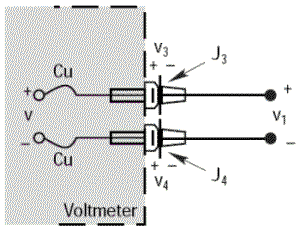
Les exemples précédents ont été présentés avec un thermocouple Cuivre/Constantan (Type T), qui peut sembler d’une utilisation facile pour les démonstrations car le cuivre est également le métal des bornes du voltmètre et cela n’induit qu’une seule jonction parasite. Effectuons le même exemple avec un thermocouple Fer/Constantan (Type J) à la place du Cuivre/Constantan.
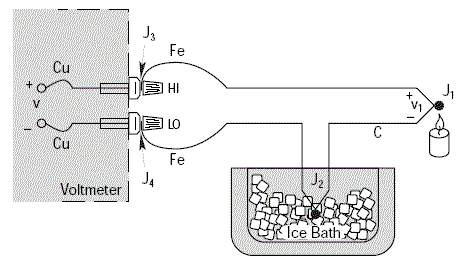
Le voltmètre indiquera une tension V égale à V1 seulement si les tensions thermoélectriques V3 et V4 sont identiques, puisqu’elles sont en opposition ; c’est-à-dire si les jonctions parasites J3 et J4 sont à la même température.
Pour éviter toute dérive de mesure, il est indispensable que les bornes de connexion du voltmètre soient à la même température.
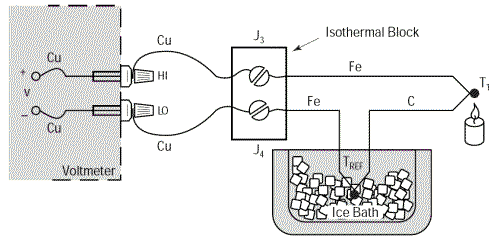
On peut éliminer ce problème en rallongeant les fils de cuivre pour ne les raccorder qu’au plus près du thermocouple avec un bloc de jonction isothermique. Un bloc de ce type est un isolant électrique mais un bon conducteur de la chaleur de manière à maintenir, en permanence, les jonctions J3 et J4 à une température identique. En procédant ainsi, nous pourrons, très facilement et sans problèmes, éloigner le thermocouple du moyen de mesure. La température du bloc isothermique n’a aucune importance puisque les tensions thermoélectriques des deux jonctions Cu-Fe sont en opposition.
Nous aurons toujours : V = α(TJ1 – TREF)
Eliminer le bain de glace fondante
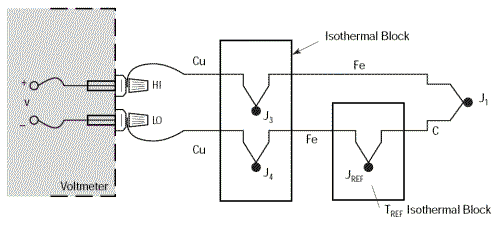
Le circuit précédent nous permet d’effectuer des mesures précises et fiables loin du thermocouple, mais quelle riche idée ce serait d’éliminer la nécessité du bain de glace fondante. Commençons par remplacer le bain de glace fondante par un autre bloc isothermique que l’on maintiendra à la température TREF.
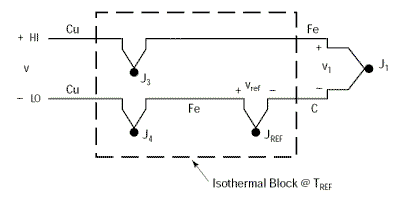
Puisque nous avons vu précédemment que la température du bloc isothermique supportant les jonctions J3 et J4 n’avait aucune importance – à condition que ces deux jonctions soient à la même température – rien ne nous empêche de réunir les deux blocs en un seul qui sera maintenu à la température TREF.
Nous aurons toujours : V = α(TJ1 – TREF)

Mais ce nouveau circuit présente, quand même, l’inconvénient de demander la connexion de deux thermocouples. Nous pouvons très bien éliminer le thermocouple supplémentaire en combinant les jonctions Cu-Fe (J4) et Fe-C (JREF). Ceci est possible grâce à la loi des métaux intermédiaires. Cette loi empirique stipule qu’un troisième métal (en l’occurrence du Fer) inséré entre les deux métaux différents d’un thermocouple n’a aucune influence sur la tension générée à condition que les deux jonctions formées par le métal additionnel soient à la même température.
Nous en arrivons donc au circuit équivalent ci-dessous dans lequel nos deux jonctions J3 et J4 deviennent la Jonction de Référence et, pour lequel, la relation : V = α(TJ1 – TREF) est toujours vérifiée.

Récapitulatif
Nous avons, dans l’ordre :
- Créé une Jonction de Référence,
- Montré que V = α(TJ1 – TREF),
- Mis la Jonction de Référence dans un bain de glace fondante,
- Supprimé le problème des bornes du voltmètre,
- Combiné le circuit de référence,
- Éliminé le bain de glace fondante
pour en arriver à un circuit simple, facile à mettre en œuvre, fiable et performant. Néanmoins, il nous faut connaître, avec précision, la température TREF du bloc de jonction isothermique pour appliquer la relation : V = α(TJ1 – TREF) et ainsi pouvoir calculer la température de la jonction J1, ce qui est toujours notre objectif. Il nous faut donc évaluer la température du bloc isothermique, ce qui sera effectué à l’aide du dispositif RT. À l’aide d’un multimètre, nous pourrons :
- Mesurer RT pour calculer TREF
- TREF en tension équivalente de jonction VREF
- Mesurer V et y ajouter VREF pour trouver V1
- Convertir V1 en température TJ1
Cette manière de procéder se nomme Compensation logicielle (Software Compensation) parce qu’elle procède par calcul pour compenser le fait que la soudure froide (ou jonction de référence) n’est pas à zéro degré. Le détecteur de température du bloc isothermique peut être n’importe quel dispositif qui comporte une caractéristique proportionnelle à la température absolue : une RTD (Resistor Température Detector), une Thermistance ou un capteur intégré.
Maintenant que nous avons utilisé soit la compensation logicielle, soit la compensation matérielle, afin d’obtenir une jonction de référence à 0°C, nous devons convertir la tension V mesurée en température.
Malheureusement, les relations entre tension et température des thermocouples ne sont pas linéaires.
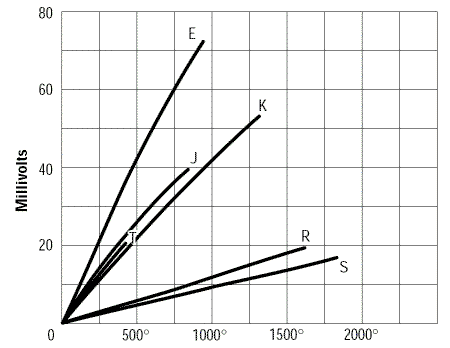
Figure 4. Tension des thermocouples en fonction de la température
| Type | Métal A (+) | Métal B (-) |
| E | Chromel | Constantan |
| J | Fer | Constantan |
| K | Chromel | Alumel |
| R | Platine | Platine 13% Rhodium |
| S | Platine | Platine 10% Rhodium |
| T | Cuivre | Constantan |
Afin de mieux visionner cette non-linéarité, regardons le coefficient de Seebeck en fonction de la température :
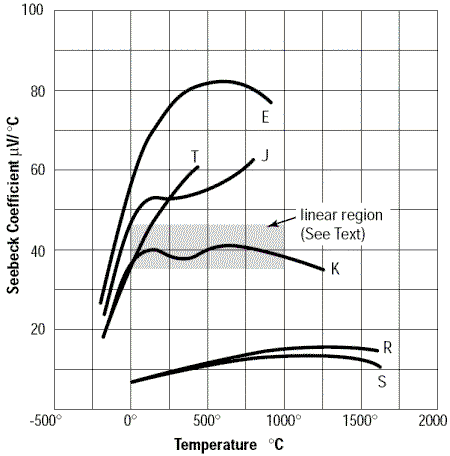
Figure 5. Coefficient de Seebeck en fonction de la température pour différents types de thermocouples
Notons que le thermocouple de type K présente une partie presque linéaire entre 0°C et 1000°C avec un coefficient de Seebeck α fluctuant autour de 40 µV/°C. Ainsi, ce type de thermocouple peut être directement exploité avec un voltmètre multiplicateur et une référence 0°C pour afficher la température avec une précision moyenne.
Calcul à partir des tables
Après avoir lu la valeur de la tension V, par exemple 8,35687 mV, avec un thermocouple de type K (Chromel/Alumel), regardons dans la table ITS-90 :
| Table ITS-90 pour Thermocouple de Type K Tension thermoélectrique en mV | |||||||||||
| °C | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 190 | 7.739 | 7.779 | 7.819 | 7.859 | 7.899 | 7.939 | 7.979 | 8.019 | 8.059 | 8.099 | 8.138 |
| 200 | 8.138 | 8.178 | 8.218 | 8.258 | 8.298 | 8.338 | 8.378 | 8.418 | 8.458 | 8.499 | 8.539 |
| 210 | 8.539 | 8.579 | 8.619 | 8.659 | 8.699 | 8.739 | 8.779 | 8.819 | 8.860 | 8.900 | 8.940 |
Nous pouvons voir que cette valeur est située entre Tinf 205 °C (8,338 mV) et Tsup 206 °C (8,378 mV). Effectuons un calcul par interpolation entre les valeurs 205 et 206 °C :
8,35687 – 8,338 = 0,01887 mV(Reliquat de tension au dessus de 205 °C)
8,378 – 8,338 = 0,040 mV pour une différence de 1 °C
0,01887 / 0,040 = 0,471 °C en plus
La température est donc de 205 + 0,471 = 205,471 °C
En résumé, l’équation est :
= 205 + [(8,35687 – 8,338) / (8,378 – 8,338)] = 205,471 °C
Soit :
$$ T\left( {^\circ C} \right) = {T_{inf}}\left( {^\circ C} \right) + \frac{{V – {V_{inf}}}}{{{V_{sup}} – {V_{inf}}}} $$
Calcul par équation polynomiale
Il est possible de calculer la température à partir de la tension thermoélectrique en ayant recours à une équation polynomiale :
$$ {T_{90}} = {c_0} + {c_1}V + {c_2}{V^2} + \cdots + {c_n}{V^n} $$
T90 = Température en °C
V = Tension thermoélectrique en mV
c = Coefficients polynomiaux
n = Ordre maximum de l’équation polynomiale
| Exemple de coefficients pour les thermocouples de type K | |||
| Température (°C) | -200 à 0 | 0 à 500 | 500 à 1372 |
| Tension (mV) | -5.891 à 0.000 | 0.000 à 20.644 | 20.644 à 54.886 |
| c0 | 0 | 0.000000E+00 | -1.318058E+02 |
| c1 | 2.5173462E+01 | 2.508355E+01 | 4.830222E+01 |
| c2 | -1.1662878E+00 | 7.860106E-02 | -1.646031E+00 |
| c3 | -1.0833638E+00 | -2.503131E-01 | 5.464731E-02 |
| c4 | -8.9773540E-01 | 8.315270E-02 | -9.650715E-04 |
| c5 | -3.7342377E-01 | -1.228034E-02 | 8.802193E-06 |
| c6 | -8.6632643E-02 | 9.804036E-04 | -3.110810E-08 |
| c7 | -1.0450598E-02 | -4.413030E-05 | 0 |
| c8 | -5.1920577E-04 | 1.057734E-06 | 0 |
| c9 | 0 | -1.052755E-08 | 0 |
| Erreur (°C) | -0.02 à 0.04 | -0.05 à 0.04 | -0.05 à 0.06 |
| Les coefficients des autres types de thermocouples sont indiqués à la fin des tables ITS-90 en annexes | |||
C’est, en quelque sorte, la fonction réciproque ou inverse de l’équation de conversion d’une tension en température :
Pour tous les types de thermocouples (sauf K à t>0°C), on a :
$$ V(mV) = \mathop \sum \limits_{i = 0}^n {\left( {{t_{90}}} \right)^i} $$
Pour les thermocouples type K aux températures supérieures à 0°C on a :
$$ V\left( {mV} \right) = \mathop \sum \limits_{i = 0}^n {\left( {{t_{90}}} \right)^i} + {a_0}{e^{{a_1}{{\left( {{t_{90}} – {a_2}} \right)}^2}}} $$
Ci = Coefficients de C0 à Cn
t90 = Température du thermocouple en °C
a0 à a2 = Coefficients spécifiques d’exponentiation uniquement pour les thermocouples de type K et pour les températures supérieure à 0 °C
e = constante des logarithmes naturels : 2.71828…
| Exemple de coefficients pour les thermocouples de type K | ||
| Température (°C) | -270 à 0 | 0 à 1372 |
| c0 | 0 | -0.176004136860e-1 |
| c1 | 0.394501280250e-1 | 0.389212049750e-1 |
| c2 | 0.236223735980e-4 | 0.185587700320e-4 |
| c3 | -0.328589067840e-6 | -0.994575928740e-7 |
| c4 | -0.499048287770e-8 | 0.318409457190e-9 |
| c5 | -0.675090591730e-10 | -0.560728448890e-12 |
| c6 | -0.574103274280e-12 | 0.560750590590e-15 |
| c7 | -0.310888728940e-14 | -0.320207200030e-18 |
| c8 | -0.104516093650e-16 | 0.971511471520e-22 |
| c9 | -0.198892668780e-19 | -0.121047212750e-25 |
| c10 | -0.163226974860e-22 | |
| Coefficients d’exponentielle pour les températures supérieures à 0 °C | ||
| a0 | 0.1185976 | |
| a1 | -0.1183432e-3 | |
| a2 | 0.1269686e+3 | |
TENSION DES DIFFERENTS THERMOCOUPLES POUR UNE TEMPERATURE DE 350 °C
| Tension calculée en mV | |||
| Type | Par table ITS-90 | Tension | Écart en % |
| B | 0,596 | 0,596 | -0,018 |
| E | 24,964 | 24,964 | 0,001 |
| J | 19,090 | 19,090 | 0,002 |
| K | 14,293 | 14,293 | 0,001 |
| N | 11,136 | 11,136 | 0,002 |
| R | 2,896 | 2,896 | 0,007 |
| S | 2,786 | 2,786 | -0,008 |
| T | 17,819 | 17,819 | -0,002 |
Au fil des années, de nombreux types de thermocouples ont été développés pour résoudre des problèmes de mesure.
Métal « noble »
Les thermocouples en métal « noble », types B, R, et S, à base de platine ou les thermocouples platine/platine-rhodium partagent des caractéristiques similaires.
Diffusion
La diffusion de vapeur métallique à températures élevées peut changer le calibrage des fils de platine, par conséquent, ils ne devraient être employés qu’à l’intérieur d’une gaine non métallique telle que la céramique de grande pureté. Une exception à cette règle est une gaine elle-même en platine, mais cette option est coûteuse.
Stabilité
Les couples à base de platine sont, de loin, les plus stables de tous. Le type S est si stable qu’on l’emploie comme « étalon » pour le calibrage de la température entre le point de solidification de l’antimoine (630,74°C) et celui de l’or (1064,43°C).
Type B
Le thermocouple B est le seul thermocouple commun qui montre une ambiguïté de double évaluation.
Les thermocouples de métal non « précieux »
À la différence des thermocouples en métal noble, les couples de métal non précieux n’ont aucune composition chimique bien précisée. On peut employer n’importe quelle combinaison des métaux qui fait que les résultats de la courbe de température est dans les limites des erreurs standard. Ceci mène à quelques combinaisons plutôt intéressantes. Le Constantan, par exemple, comme vu précédemment, n’est pas un alliage avec des proportions bien définies, mais un nom générique pour des alliages de cuivre-nickel.
Type E
Le thermocouple du type E est approprié aux mesures de basses températures en raison de son coefficient de Seebeck élevé (58 µV/°C), de sa basse conductivité thermique et de sa résistance à la corrosion. Le coefficient de Seebeck pour le type E est le plus grand de tous les thermocouples standards, qui le rend utile pour détecter de petits changements de température.
Type J
Le fer, l’élément positif dans un thermocouple J est un métal peu coûteux, mais rarement très pur. Les thermocouples J sont sujets à des dispersions de caractéristiques en raison des impuretés dans le fer. Néanmoins, le thermocouple J est populaire en raison de son coefficient de Seebeck élevé et son bas prix. Le thermocouple de J devrait jamais être utilisé au-dessus de 760°C à cause d’une transformation magnétique brusque qui peut causer la décalibration même lors du retour à de plus basses températures.
Type T
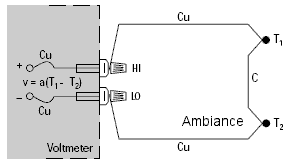
Le type T a la particularité d’avoir un fil de cuivre. Avantage important qui permet, dans des cas de surveillance de différence de température, de s’affranchir de la compensation de soudure froide en montant deux thermocouples de type T en série.
Types K et N
Le type K a toujours été un thermocouple très employé. Il convient à des mesures de température élevée grâce à sa résistance à l’oxydation. Le thermocouple du type N gagne en popularité en remplacement du type K. Il a un résultat légèrement inférieur (coefficient de Seebeck plus faible) que le type K, mais une résistance encore plus élevée à l’oxydation. La courbe de rendement de thermocouple du type N dépend de la taille de fil, et il y a deux courbes caractéristiques distinctes de Nicrosil-Nisil suivant la taille du fil
La même année que Seebeck découvrit la thermo-electricité, Humphrey Davy (1778-1829) annonça que la résistivité des métaux montrait une dépendance marquée à la température. Cinquante ans après, William Siemens utilise du platine dans un thermomètre à résistance. Son choix propice est prouvé par l’utilisation du platine comme élément principal dans les thermomètres à résistance de grande précision. En fait, le capteur de température à résistance de platine, ou PRTD (Platinium Resistance Temperature Detector), est employé aujourd’hui du point triple de l’hydrogène (-259,34 °C) au point de congélation de l’argent (961,78°C). Le platine convient particulièrement, car il peut supporter cette grande plage de températures tout en maintenant une excellente stabilité et une altération quasiment nulle.
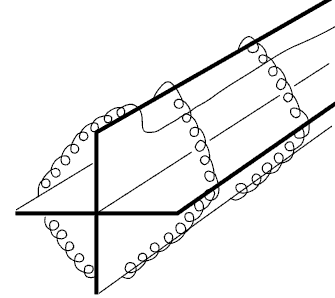
En 1932, C.h. Meyers proposa la construction d’un capteur de température à résistance (RTD) composé d’un enroulement hélicoïdal de platine sur un support croisé de mica, le tout à l’intérieur d’un tube de verre. Ce système réduit au minimum la contrainte sur le fil tout en maximisant la résistance. Bien que cette construction produise un élément très stable, le contact thermique entre le platine et le point à mesurer est de mauvaise qualité avec, comme conséquence, un temps de réponse thermique important. La fragilité de la structure limite, aujourd’hui, son utilisation à celle d’un outil de laboratoire.
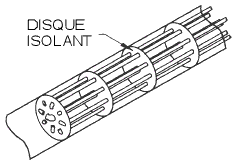
Un autre outil de laboratoire a remplacé la conception de Meyer. C’est l’élément en « cage d’oiseau » proposé par Evans et Burns. Les contraintes induites de résistance provoquées par le temps et la température sont ainsi réduites au minimum et la « cage d’oiseau » devint la norme de laboratoire. Sa structure fragile et sa sensibilité aux vibrations ne la destine pas aux environnements industriels.
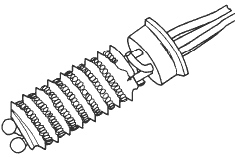
Des techniques de construction plus solides sont montrées par les figures ci-contre : un fil de platine bifilaire est enroulé sur une bobine de verre ou de céramique. L’enroulement bifilaire réduit l’induction magnétique et son bruit relatif. Une fois que le fil est enroulé sur la bobine, l’ensemble est alors scellé avec du verre fondu. À moins que les coefficients de dilatation du platine et de la bobine s’assortissent parfaitement, la dilatation du fil aura pour résultat un changement de résistance, avec pour conséquence un changement permanent possible de la résistance du fil.
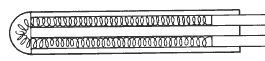
Il existe des versions de RTD qui offrent un compromis entre la cage d’oiseau et la spirale scellée. Une telle approche emploie une spirale de platine hélicoïdale enroulée sur un cylindre en céramique et maintenue par l’intermédiaire de verre fritté.

Les techniques de fabrication modernes utilisent un film de platine ou métallique déposé sur un substrat plat de céramique gravé à l’eau-forte, ajusté par laser et scellé. Le film RTD offre la réduction substantielle du délai d’assemblage et a l’avantage d’une valeur de résistance accrue pour une taille donnée. En raison de la technologie de fabrication, la taille des dispositifs est petite, avec une inertie thermique faible ; ils peuvent répondre rapidement aux changements de température.

Les RTD à film, quant à elles, sont un peu moins stables que les RTD filaires mais, en contrepartie, leurs avantages de taille, de coût de production et facilité d’utilisation font qu’elles sont très largement employées.
Tous les métaux produisent un changement positif de résistance pour un changement positif de la température, ce qui est la fonction principale d’une RTD. L’erreur du système est réduite au minimum quand la valeur nominale de la résistance de RTD est grande ; ceci implique un fil métallique avec une résistivité élevée.
| Résistivité des métaux des RTD | ||||
| Métal | Symbole | Résistivité Ω·cm/f | Résistivité Ω·mm²/m | Résistivité siemens |
| Or | Au | 13 | 2,1612e-2 | 4,6272e+7 |
| Argent | Ag | 8,8 | 1,4629e-2 | 6,8356e+7 |
| Cuivre | Cu | 9,26 | 1,5394e-2 | 6,496e+7 |
| Platine | Pt | 59 | 9,8083e-2 | 1,0195e+7 |
| Tungstène | W | 30 | 4,9873e-2 | 2,0051e+7 |
| Nickel | Ni | 36 | 5,9847e-2 | 1,6709e+7 |
En raison de leurs faibles résistivités, l’or et l’argent sont rarement employés comme éléments de RTD.
Le tungstène a une résistivité relativement élevée, mais est réservé pour des applications à très hautes températures parce qu’il est extrêmement fragile et difficile à travailler.
Le cuivre est employé de temps en temps comme élément de RTD, sa basse résistivité nécessite une plus grande longueur qu’un élément de platine, mais sa linéarité et son prix réduit en font une alternative économique. Sa limite supérieure de température est seulement d’environ 120 °C.
Les RTD les plus communes sont faites de platine, nickel, ou alliages de nickel. Les fils en alliage de nickel sont économiques et employés sur une gamme de température limitée, mais ils sont non linéaires et tendent à dériver avec le temps.
Pour l’intégrité des mesures, le platine est le choix évident.
Les valeurs communes des résistances des RTD s’étendent de 10 ohms pour le modèle cage d’oiseau à plusieurs milliers d’ohms pour les RTD à film métallique. La valeur la plus commune est de 100 ohms à 0 °C, appelé coefficient R0. De telles RTD sont appelées Pt 100.
Le coefficient de température normalisé DIN 43760 du fil de platine est : α = 0.00385. Pour une résistance de 100 ohms à 0 °C, ceci correspond à + 0,385 ohm par °C (α européen). α est donc la pente moyenne de 0°C à 100°C $$ \alpha = \frac{{{R_{100}} – {R_0}}}{{{R_0} \times 100^\circ C.}} $$. Il existe une grande variété de RTD qui ont des coefficients α différents et des valeurs ohmiques à 0°C précisés dans leurs caractéristiques techniques. La RTD la plus utilisée est celle ayant un coefficient α de 0.00385 et une valeur ohmique à 0°C de 100 Ω. Elle est dénommée Pt100.
| Valeurs de quelques RTD | ||
| R à 0°C (Ω) | α (Ω/Ω/°C) | Sensibilité moyenne (Ω/°C) |
| 25.5 | 0.00392 | 0.1 |
| 100 | 0.00392 | 0.392 |
| 100 | 0.00391 | 0.391 |
| 100 | 0.00385 | 0.385 |
| 200 | 0.00385 | 0.770 |
| 470 | 0.00392 | 1.845 |
| 500 | 0.00392 | 1.963 |
| 500 | 0.00391 | 1.955 |
| 500 | 0.00385 | 1.925 |
| 1000 | 0.00385 | 3.850 |
| 1000 | 0.00375 | 3.750 |
| 10000 | 0.00385 | 38.50 |
| Standards internationaux DIN 43760 (IEC 751, BS-1904, JIS C1604) | ||
| Paramètre | Class A | Class B |
| R0 | 100Ω ±0,06% | 100Ω ±0,12% |
| Alpha, α | 0,00385 ±0,000063 | 0,00385 ±0,000063 |
| Plage | -200°C à 650°C | -200°c à 850°C |
| Res, RT | ±(.06+.0008|T|-2e-7T2) | ±(.12+.0019|T|-6e-7T2) |
| Temp, T | ±(0.3+0.002|T|)°C | ±(0.3+0.005|T|)°C |
Le choix de la méthode de connexion et de l’interface électronique dépend de la précision de mesure recherchée.
Une RTD peut être utilisée selon 3 modes de connexion : 2 fils, 3 fils ou 4 fils.
Mesures en 2 fils
Le plus simple mais induit une erreur proportionnelle à la longueur du câble utilisé pour la connexion. Un câble standard AWG24 (85 Ω/km) introduit une erreur de l’ordre de 0.42°C par mètre de connexion pour une sonde RTD Pt100.

La pente et la valeur absolue sont de petits nombres, particulièrement quand nous considérons le fait que les fils de mesure reliés à la sonde peuvent être de plusieurs ohms ou même dizaines d’ohms. Une petite impédance de fil peut contribuer à une erreur significative de notre mesure de la température. Une impédance de fil de 10 ohms implique une erreur de 10/0,385 soit environ 26°C dans ce cas.

Une des méthodes pour éviter ce problème est l’utilisation d’un moyen de mesure en pont. La mesure par un pont, ici un pont de Wheatstone, est une indication indirecte de la résistance de la RTD. Le pont nécessite quatre fils de raccordement, une source extérieure, et trois résistances qui ont un coefficient de température nul.

Mesures en 3 fils
Le mode « 3 fils » assure bien souvent une qualité de mesure suffisante pour la plupart des applications industrielles. Il repose sur l’hypothèse d’égalité des résistances des 3 fils. L’utilisation d’un câble AWG18 (21 Ω/km) introduit moins de 0.4°C d’erreur pour 100 m de connexion.


Pour éviter de soumettre les trois résistances du pont à la même température que la RTD, on sépare celle-ci du pont par une paire de fils de liaison. Ces fils recréent le problème que nous avons eu précédemment : l’impédance des fils de liaison affecte la lecture de la température. Cet effet peut être réduit au minimum en employant une configuration de pont en trois fils. Si les fils A et B sont de la même longueur, leurs effets d’impédance s’annuleront parce que chacun est dans une partie opposée du pont. Le troisième fil, C, agit comme mesure dans lequel il ne circule aucun courant. Le pont de Wheatstone représenté sur la figure 41 crée un rapport non linéaire entre le changement de résistance et le changement de tension de mesure du pont. Ceci nécessite une équation additionnelle pour convertir la tension de mesure du pont en impédance équivalente de RTD.

Mesures en 4 fils
C’est le montage offrant la meilleure précision, la mesure de tension étant effectuée au niveau de la partie active de la sonde avec une interface électronique haute impédance. Les résistances des câbles de connexion n’interviennent plus dans l’erreur de la mesure.

La meilleure technique est d’utiliser une source de courant connu et de mesurer, à distance, la tension aux bornes de la RTD. Comme aucun courant ne circule dans les fils de mesure de tension, il n’y a aucune chute de tension et, donc, aucune erreur de mesure de résistance. La tension lue sur le voltmètre est directement proportionnelle à la valeur de la résistance de la RTD. Les trois résistances du pont sont remplacées par une résistance de référence permettant de connaître avec précision le courant généré (figure 42). L’inconvénient est de nécessiter un fil de plus que le pont à 3 fils. C’est un petit prix à payer pour obtenir avec exactitude la mesure de la résistance.

Les capteurs Pt100 (platine 100 Ω (PRTD)) sont plus linéaires que les thermocouples :

Figure 6 Evolution du coefficient de linéarité d’un TC type S et d’une Pt100
La relation entre la température et la valeur ohmique des RTD a été calculée par Callendar puis, plus tard, affinée par Van Dusen ; c’est pourquoi cette équation est nommée Callendar-Van Dusen (CVD) :
$$ {R_T} = {R_0} + {R_0}\alpha \left[ {T – \delta \left( {\frac{T}{{100}} – 1} \right)\left( {\frac{T}{{100}}} \right) – \beta \left( {\frac{T}{{100}} – 1} \right)\left( {\frac{{{T^3}}}{{100}}} \right)} \right] $$
Avec RT = résistance à T°C, R0 = résistance à 0°C, α = coefficient de température à 0°C en Ω/Ω/°C, δ = coefficient de linéarisation, β = deuxième coefficient de linéarisation pour les valeurs négatives de température (β = 0 pour T > 0°C).
Cette équation a été transformée pour pouvoir être utilisée plus facilement avec les coefficients A, B et C donnés par la norme DIN 43760 (IEC 751) et les fiches techniques des composants :
$$ {R_T} = {R_0}\left[ {1 + AT + B{T^2} – C\left( {T – 100} \right){T^3}} \right] $$
C=0 pour T>0°C.
| Coefficients pour différents α | |||
| Coefficient | Valeur | Valeur | Valeur |
| α | 0,003850 | 0,003926 | 0,003911 |
| δ | 1,4999 | ||
| β | 0,10863 | ||
| A | 3,9083e-3 | 3,9848e-3 | 3,9692e-3 |
| B | -5,775e-7 | -5,870e-7 | -5,8495e-7 |
| C | -4,18301e-12 | -4,000e-12 | -4,2325e-12 |
Ces trois valeurs α représentent les trois principales spécifications pour les RTD
- 0,003850 Ω/Ω/°C : Normalisation DIN 43760, IEC 751 et autres spécifications internationales, nommé Standard Européen.
- 0,003926 Ω/Ω/°C : Nécessite un platine pur à 99,999% ou mieux, nommé Standard Américain.
- 0,3911 Ω/Ω/°C : Souvent nommé Standard Industriel U.S.
L’équation de CVD calcule la résistance en fonction de la température ; ce qui est l’inverse des utilisations les plus courantes : température en fonction de la résistance. Pour convertir la valeur de résistance de la RTD en température, on est obligé d’utiliser une équation quadratique du 2e degré, qui est, en quelque sorte, la réciproque de l’équation CVD, mais uniquement pour les températures supérieure à 0°C :
$$ T = \frac{{ – A + \sqrt {{A^2} – 4B\left( {1 – \frac{{{R_T}}}{{{R_0}}}} \right)} }}{{2B}} $$
Pour les températures inférieures à 0°C, l’équation CVD est trop complexe à résoudre, aussi l’emploi des méthodes numérique s’impose. La plus précise consiste à chercher numériquement la racine de l’équation de CVD ; autrement dit de résoudre l’équation suivante :
$$ f\left( T \right) = {R_0}\left[ {1 + AT + B{T^2} + C\left( {T – 100} \right){T^3}} \right] – {R_T} = 0 $$
La méthode la plus adaptée est celle de la tangente (ou algorithme de Newton). Cette méthode présente l’avantage de converger à coup sûr à condition d’avoir bien encadré la racine dans un intervalle donné, ce qui est réalisable connaissant la sensibilité moyenne d’une RTD. Cette méthode oblige également de connaître la dérivée de l’équation de CVD, aisément calculable :
$$ \frac{{df\left( T \right)}}{{dT}} = {R_0}\left[ {A + 2BT + 4C{T^3} – 300C{T^2}} \right] $$
Enfin, il faut être sûr que l’équation n’a qu’une seule racine, ce qui est le cas de l’équation de CVD. L’algorithme, simple, se trouve dans tous les livres sur les méthodes numériques. Il consiste à déterminer, pour un point de départ $$ {{t_0}} $$, la tangente en ce point $$ f’\left( {{t_0}} \right) $$ qui coupe la courbe en un nouveau point $$ {{t_1}} $$. En ce point, on recalcule la tangente $$ f’\left( {{t_1}} \right) $$ qui coupe à son tour la courbe en un point $$ {{t_2}} $$, etc… jusqu’au moment où l’écart entre deux points successifs t_i soit plus petit que le critère d’arrêt (défini par ε). Le programme « RTD.xls » utilise cet algorithme. Voici le code source :
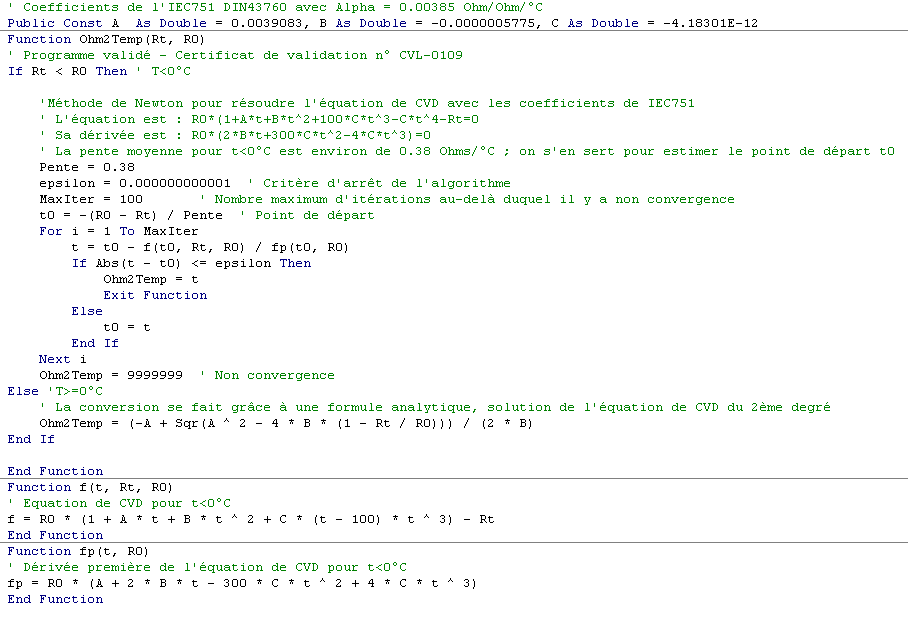
Les systèmes de thermomètre à résistance sont sensibles à trois types d’erreurs :
- Les tolérances inhérentes à la résistance elle-même
- Les gradients de température entre le thermomètre et le milieu à mesurer
- Les erreurs et défauts présents dans la liaison entre la sonde et l’instrument de mesure.
Quelques sources d’erreur sont électriques ; d’autres résultent de la construction mécanique du thermomètre. Les sources d’erreur potentielles incluent l’interchangeabilité et la conformité. La conformité indique de quelle quantité il est permis de dévier de la courbe standard. La conformité a deux composantes : une tolérance à la température de référence, habituellement 0°C, et une tolérance sur la pente.
Ces écarts possibles sont définis par la normalisation. Par exemple, la norme DIN 43760 classe B, exige le calibrage à moins de 0,12Ω (0.3°C) à 0°C, mais permet à la courbe de s’écarter du nominal 0,00385 de ±0.000012 Ω/Ω/°C. Ceci peut donner des écarts de 0.8°C à 100°C, 1.3°C à 200°C, et jusqu’à 3.8°C à 700°C.
Il est donc important de connaître, avec précision, les tolérances du moyen utilisé.
Un thermomètre à résistance est une sonde passive ; il nécessite le passage d’un courant de mesure afin de produire un signal utile. Ce courant de mesure chauffe l’élément et élève sa température. Des erreurs en résulteront à moins que la chaleur supplémentaire ne soit absorbée.
L’auto-échauffement est exprimé en mW/°C, qui est la puissance en milliwatts (1000.RI²) qui élève la température interne de la sonde de 1°C. Plus le nombre de mW/°C est élevé, moins le phénomène est important puisqu’il faut plus de puissance pour la même élévation de température.
Comme exemple, supposons un courant de mesure de 5 mA à travers des sonde Pt100 dans une ambiance à 100°C. Les spécifications (CEI751) indiquent 50 mW/°C dans l’eau se déplaçant à 1 m/sec. La quantité de la chaleur produite est : 1000 mW * (0,005 A)² * (138,5Ω) = 3,5 mW ; l’erreur d’auto-échauffement est : (3,5 mW)/(50 mW/°C) = 0.07°C, soient 0.07% de la température du milieu. 5 mA est un courant élevé. Les moyens de mesure modernes utilisent des courants de mesure très faibles, de l’ordre de 100μA et même moins. Ce qui, dans le cas précédent, donnerait une erreur d’élévation de température de seulement (0.00138 mW)/(50 mW/°C) = 0,000027°C, ce qui est négligeable.
Attention, l’erreur résultante est inversement proportionnelle à la capacité du thermomètre d’évacuer la chaleur supplémentaire ; ce qui dépend des matériaux, de la construction, et de l’environnement de thermomètre.
Le plus mauvais cas se produit quand une résistance de valeur élevée est dans un petit corps. Les RTD film, avec peu de superficie pour absorber la chaleur, en sont un exemple.
L’auto-échauffement dépend également du milieu dans lequel le thermomètre est immergé. L’erreur dans l’air immobile peut être 100 fois plus grande que dans l’eau en mouvement.
Une constante de temps indique la réponse d’un thermomètre au changement de température. Une expression commune est le temps que met un thermomètre pour refléter 63,2% d’un échelon de température dans l’eau en mouvement. Dans le cas d’un changement de 90% on parlera du « T90 ».
La vitesse de réponse dépend de la masse du thermomètre et du taux des transferts thermiques entre la surface externe de l’élément et le milieu dans lequel il est plongé. Une petite constante de temps réduit les erreurs dans un système sujet aux changements rapides de température.
Mesurer une grandeur, c’est la comparer à une grandeur de même espèce prise comme référence. Cette dernière constitue une unité de mesure ; l’ensemble des unités de mesures légales forme un système appelé Système International (SI).
En métrologie, domaine des connaissances relatives aux mesurages, le mot mesure a de nombreuses significations qu’il importe de préciser dès maintenant ; il peut désigner :
- une valeur : la mesure d’une distance est de 100 mètres
- un résultat : mesure approchée à 1 % près
- une action : réaliser une mesure électrique
- un instrument: une mesure de capacité
Pour éviter toute ambiguïté, il est préférable de parler respectivement de valeur d’une grandeur, de résultat de mesurage, de mesurage et de mesure matérialisée. Toutefois, lorsqu’aucune confusion n’est possible, on appelle mesure l’expression d’un résultat de mesurage.
Un étalon est un instrument de mesurage destiné à définir ou matérialiser, conserver ou reproduire l’unité de mesure d’une grandeur (ou un multiple ou un sous-multiple de cette unité).
Selon l’usage qui en est fait, plusieurs sortes d’étalons sont fabriquées. Pour une grandeur déterminée, l’étalon primaire est celui qui présente les plus hautes qualités métrologiques; il n’est jamais utilisé directement pour des mesurages en dehors de sa comparaison avec des étalons secondaires. À partir d’un étalon secondaire sont réalisés des étalons de travail qui sont utilisés pour vérifier les instruments de mesurage.
On appelle erreur de mesurage la discordance entre le résultat du mesurage et la valeur de la grandeur mesurée.
Cette valeur peut être la valeur vraie ou, si celle-ci n’est pas connue (cas le plus fréquent), la valeur conventionnellement vraie de la grandeur, ou encore la moyenne arithmétique des résultats d’une série de mesurages. Cette discordance peut avoir des causes variées et, en général, on ne peut en déterminer qu’une limite supérieure, appelée incertitude de mesurage.
C’est une erreur qui reste constante en valeur absolue et en signe lorsque plusieurs mesurages d’une même grandeur fixe sont réalisés dans les mêmes conditions.
Les causes des erreurs systématiques peuvent être connues ou non. Si une telle erreur peut être déterminée par le calcul ou par l’expérience, on apporte une correction appropriée au résultat du mesurage. Si une erreur systématique ne peut pas être déterminée mais si sa valeur peut être supposée suffisamment petite par rapport à l’imprécision de mesurage, on la traite comme une erreur fortuite ; au contraire, si elle est supposée très supérieure à l’imprécision de mesurage, elle est évaluée approximativement et prise en compte dans le calcul de l’erreur.
Exemple d’erreur systématique : mesurage d’une masse à l’aide d’une masse marquée supposée égale à 1 kg, alors que sa masse vraie est 1,005 kg.
C’est une erreur qui varie de façon imprévisible en valeur absolue et en signe lorsqu’on effectue un grand nombre de mesurages d’une même grandeur dans des conditions pratiquement identiques. On ne peut pas tenir compte d’une erreur fortuite en apportant une correction au résultat brut du mesurage. À la fin d’une série de mesurages, on peut seulement fixer une limite supérieure pour cette erreur. Une erreur fortuite est souvent appelée erreur accidentelle ou erreur aléatoire.
C’est une erreur souvent grossière qui résulte d’une exécution incorrecte du mesurage. Par exemple, elle peut être due à une lecture fausse, ou à l’usage d’un instrument devenu défectueux, ou encore au mauvais emploi d’un instrument. Elle n’est pas prise en compte lors de l’analyse des mesures.
Au cours d’un mesurage déterminé plusieurs erreurs peuvent être commises : erreur due à l’appareil de mesurage, erreur due aux accessoires de l’appareil de mesurage, erreur de lecture, etc. Ces erreurs sont appelées erreurs partielles. L’incertitude de mesurage doit permettre de tenir compte de toutes les erreurs partielles en les composant selon une certaine loi qui est 2 fois la racine carrée de la somme des carrés des erreurs partielles.
C’est la différence algébrique dx entre le résultat du mesurage X et la valeur de comparaison qui peut être la valeur vraie Xv ou conventionnellement vraie, ou la moyenne arithmétique x des résultats d’une série de mesurages. Dans le premier cas, l’erreur absolue est dite véritable (dx = X – Xv) ; dans le deuxième, elle est dite apparente (dx = X – x).
C’est le quotient de l’erreur absolue et de la valeur de comparaison utilisée pour le calcul de l’erreur absolue (dx/Xv ou dx/x).
Dans une série de n mesurages d’une même grandeur, on caractérise la dispersion des résultats obtenus autour de la moyenne par l’écart quadratique moyen σ qui est donné par la formule ci-dessous :
$$ \sigma = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^n {{\left( {{x_i} – \bar x} \right)}^2}}}{{n – 1}}} $$
Pour un grand nombre de mesures, si l’on désigne par $$ x_i $$ le résultat de mesurage de numéro i (i = 1,2,3,…,n) et par $$ \bar x $$ la moyenne $$ \bar x = \frac{{\mathop \sum \nolimits_{i = 1}^n {x_i}}}{n} $$.
L’augmentation du nombre de mesurages permet de diminuer l’importance des erreurs fortuites et une moyenne des résultats peut être acceptée comme résultat d’une série de mesurages.
Le « GUM » (Guide of Uncertainties Measurements) préconise toutefois de pondérer cet écart-type par un coefficient, dit « de Student », noté s, si le nombre de mesures est plus petite que ou égal à 5.
- Pour 3 mesures, s=9.2
- Pour 4 mesures, s=6.6
- Pour 5 mesures, s=5.5
La formule de l’écart-type devient alors :
$$ \sigma = \frac{s}{{3\sqrt n }}\sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^n {{\left( {{x_i} – \bar x} \right)}^2}}}{{n – 1}}} $$
Attention à ne pas confondre l’écart-type avec l’étendue qui est la différence entre la valeur minimum et la valeur maximum des grandeurs mesurées : $$ e = {x_{max}} – {x_{min}} $$.
Pour un appareil électromécanique, les principales erreurs de base sont dues aux frottements d’éléments mobiles sur des parties fixes, à l’inertie mécanique, à l’inertie thermique, à des erreurs de lecture, notamment à l’erreur de parallaxe (si l’index est à une certaine distance de la surface de l’échelle et que l’observateur ne peut se placer normalement à cette surface).
Une courbe d’étalonnage est fournie par le constructeur pour les appareils de qualité : elle exprime la correspondance entre les valeurs de la grandeur mesurée et les valeurs indiquées par l’appareil. Éventuellement, des courbes de corrections permettent de corriger les résultats obtenus lorsqu’une ou plusieurs grandeurs d’influence ne sont pas dans les conditions de référence.
Plusieurs qualités sont à considérer pour juger un appareil de mesure.
La justesse caractérise l’aptitude d’un appareil à donner des indications égales à la valeur vraie de la grandeur mesurée, c’est-à-dire non entachées d’erreurs systématiques
La fidélité caractérise l’aptitude d’un appareil à donner des indications concordantes, donc non entachées d’erreurs fortuites pour une même grandeur mesurée.
La sensibilité exprime quelle est la plus petite quantité dx qui peut être mesurée pour une valeur déterminée x de la grandeur mesurée. Cette sensibilité peut être constante le long de l’échelle. On remarquera que la sensibilité est d’autant plus grande que le nombre dx est faible.
L’hystérésis ou réversibilité caractérise l’aptitude d’un appareil à donner la même indication lorsqu’on atteint une même valeur de la grandeur mesurée par valeurs croissantes ou par valeurs décroissantes.
Le temps de réponse d’un appareil est le temps qui s’écoule entre une variation brusque de la grandeur à mesurer et l’instant où l’instrument donne une indication définitive de la nouvelle valeur de la grandeur.
La précision d’un appareil de mesure est égale au rapport dx/x de l’erreur globale dx et de la valeur x de la grandeur à mesurer. Elle caractérise la qualité d’un instrument du point de vue des erreurs; la précision est d’autant plus grande que les indications sont plus proches de la valeur vraie (c’est-à-dire que dx est petit).
La résolution, employée pour les appareils à affichage numérique, exprime la plus petite valeur qui peut être affichée. À ne pas confondre avec la sensibilité ou la précision.
L’étendue de mesure d’un appareil est l’ensemble des valeurs pour lesquelles les indications obtenues ne sont pas entachées d’une erreur supérieure à l’erreur maximale tolérée. Certains instruments peuvent avoir plusieurs étendues de mesure.
Le calibre d’un appareil est la valeur de la grandeur à mesurer qui correspond à la limite supérieure de l’étendue de mesure. Par exemple, pour un ampèremètre, si cette limite supérieure est 5 A, on dit que son calibre est de 5 A.
Un appareil de mesure (et ses accessoires) est caractérisé au moyen d’un nombre, appelé indice de classe. Celui-ci représente la limite supérieure de l’erreur absolue intrinsèque (c’est-à-dire due à l’appareil seul utilisé dans les conditions de référence) exprimée en centièmes de la plus grande indication que peut donner l’appareil.
Ainsi, par exemple, un ampèremètre de classe 0,2 est un appareil dont l’erreur absolue intrinsèque ne dépasse pas 0,2 % de son indication la plus grande, lorsqu’il est utilisé dans des conditions normales. Si cet ampèremètre comporte 100 divisions, cette erreur absolue 0,2 intrinsèque est donc égale ou inférieure à 0,2/100*100= 0,2 division.
Pour un appareil à plusieurs calibres, ce résultat reste le même quel que soit le calibre ; en revanche, l’expression de cette erreur en ampères change avec celui-ci puisque 0,2 division d’une graduation qui en comporte 100 représente 0,2/100 du calibre (0,002 A pour le calibre 1 A) ; 0,01 A pour le calibre 5 A).
Les valeurs des indices de classe sont fixées par la norme NF C 42-100. Des appareils de même indice de classe sont dits de même classe de précision. Les appareils de classe 0,1 ou 0,2 sont dits étalons ; ceux de classe 0,5 sont des appareils de laboratoire. Les appareils de classe 1,5 ou 2,5 sont des appareils de contrôle.
Arrondir un nombre décimal c’est donner sa valeur la plus proche de la précision désirée. Selon l’arrondi souhaité, on regarde le chiffre qui est juste après :
- si celui-ci est 0 ; 1 ; 2 ; 3 ou 4 le chiffre à retenir pour l’arrondi reste inchangé
- si celui-ci est 5 ; 6 ; 7 ; 8 ou 9 le chiffre à retenir pour l’arrondi est augmenté de 1
Exemples :
0.9273426 ➨ 0.927343 ; 0.9 ➨ 1 ; 2.5 ➨ 3 ; 1.34 ➨ 1.3